Computer Algorithms
A history of algorithms and their role in proving God's number.
Morwen Thistlethwaite (1980)
In 1979, Morwen Thistlethwait devised a method for solving the cube that starts by building a 2x2x3 block [1].
- Build a 2x2x3 block at bl.
- Orient all remaining edges.
- Solve the FU, FL, and FD edges.
- Solve the UFL and DFL corners.
- Solve the right side layer edges.
- Solve the right side layer corners.
In 1980, Thistlethwaite created a new strategy for solving the cube [2, 3, 4]. This is the algorithm that influenced many later methods for solving the cube in as few moves as possible. This algorithm was stated to take a maximum of 52 moves and was later reduced to below 50 moves.
- Orient all edges. (Group 1: <L, R, F, B, U2, D2>). Moves: 7.
- Move L/R edges to L/R and orient all corners to L/R. (Group 2: <L, R, F2, B2, U2, D2>). Moves: 13.
- Move all edges into their correct inner slices and position all corner stickers to their matching or opposite layers. (Group 2: <L2, R2, F2, B2, U2, D2>). Moves: 15.
- Solve using the move group from step 3. Moves: 17.

Hans Kloosterman (1990)
In 1990, Hans Kloosterman improved upon Thistlethwaite's algorithm [5, 3, 6, 4]. A similar structure is followed, but later steps are combined and the pieces of the 90 degree turns in Group 2 are within their correct layers. This algorithm reduced the maximum number of moves to 42.
- Orient all edges. (Group 1: <L, R, U, D, F2, B2>)
- Move all U/D pieces to U/D and orient all corners to U/D. (Group 2: <U, D, L2, R2, F2, B2>)
- Move U and D pieces to their correct layers.
- Finish.
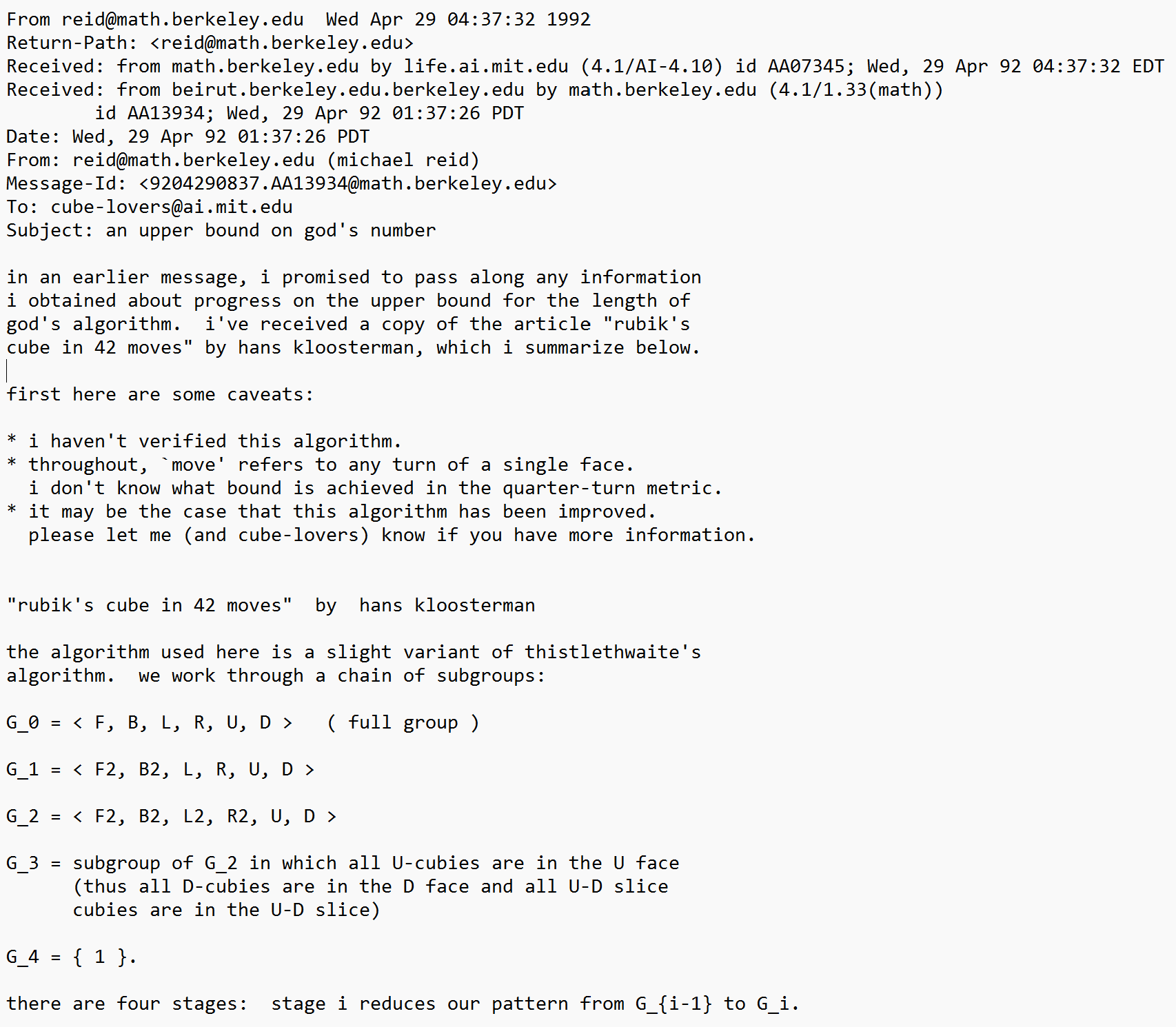
Herbert Kociemba (1992)
In 1992, another improvement upon Thistlethwaite's algorithm was published in Cubism For Fun [7, 8]. Herbert Kociemba combined steps of Thistlethwaite's algorithm to reduce it to a two stage process. It was stated that all tested positions were solved in a maximum of 21 moves. However, a complete proof wasn’t included with the publication.
- Orient edges, move all U/D pieces to U/D, and orient all corners to U/D. (Group 1: <U, D, L2, R2, F2, B2>)
- Solve using the move group from step 1.
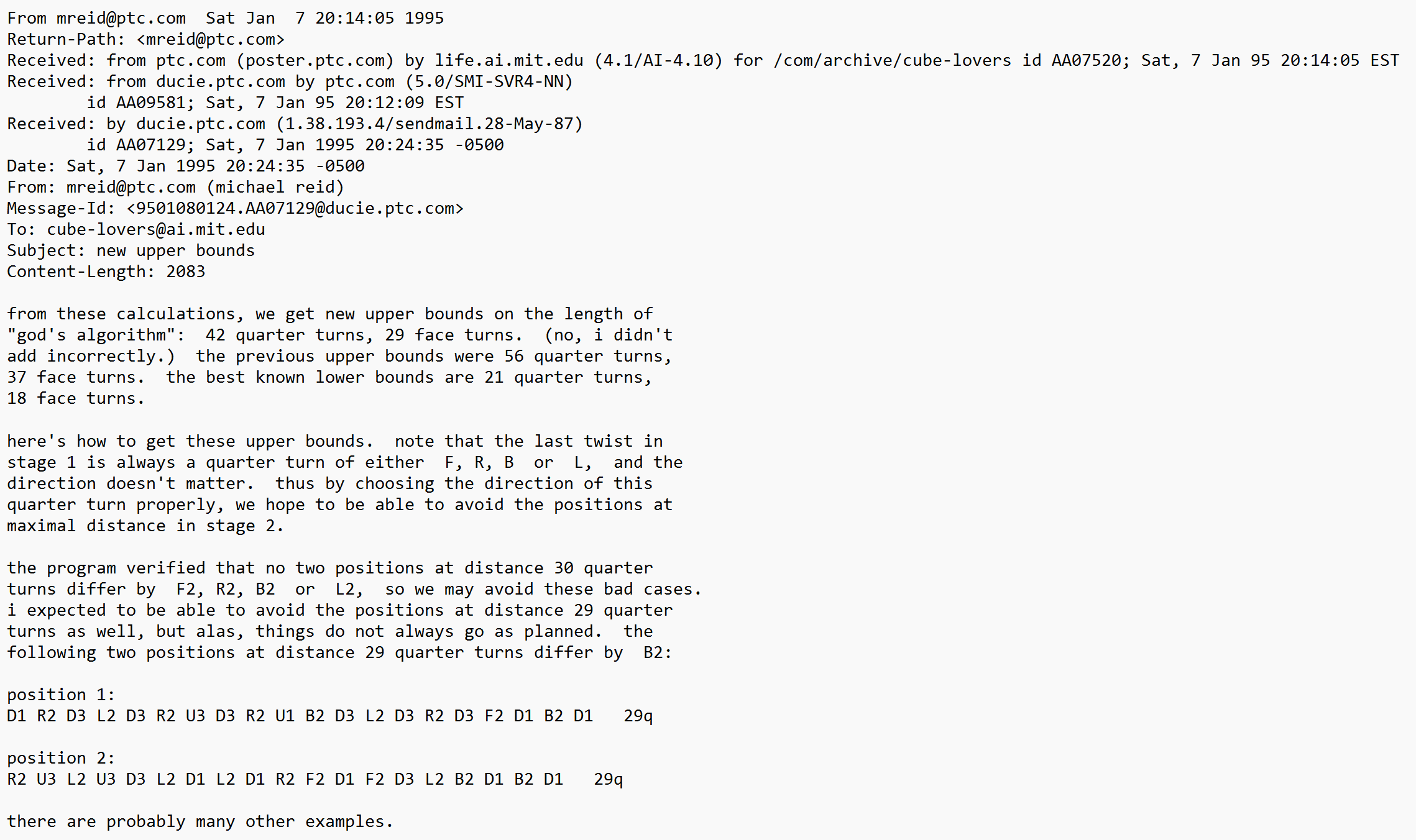
Mike Reid (1992, 1994)
On May 22, 1992, Mike Reid submitted an alternative algorithm to the Cube Lovers mailing list [9, 3, 4]. Using this algorithm, Reid reduced the upper bound to 39 moves.
- Solve a 2x2x2 block at dbl. (Group 1: <U, R, F>). Moves: 8.
- Orient all edges and corners and move all U/D pieces to U/D. (Group 2: <U, R2, F2>). Moves: 13.
- Solve using the move group from step 2. Moves: 19.

In 1995, Reid ran a calculation on the <U, D, F2, R2, B2, L2> group, reducing the maximum to 29 moves [10, 4].
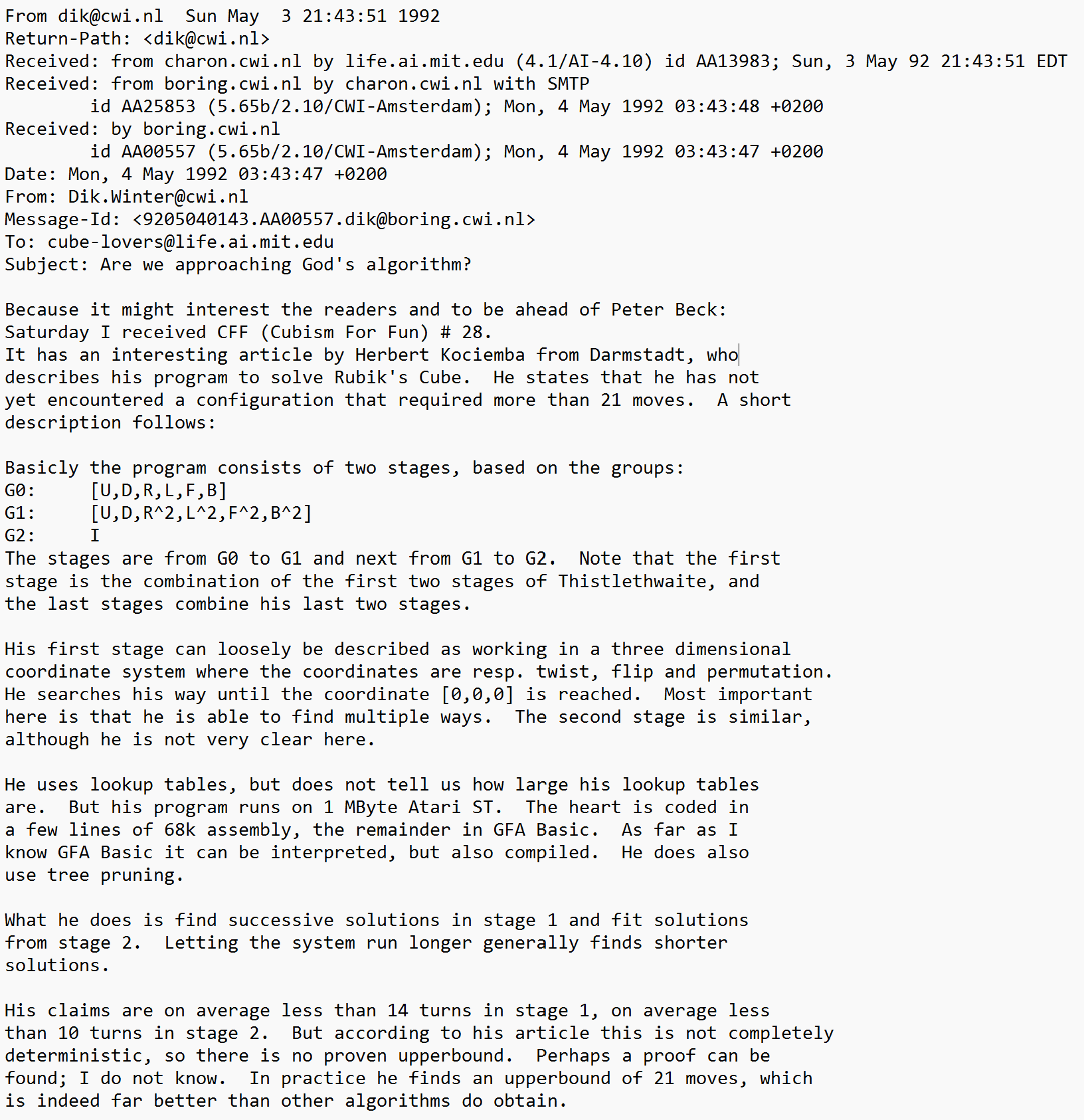
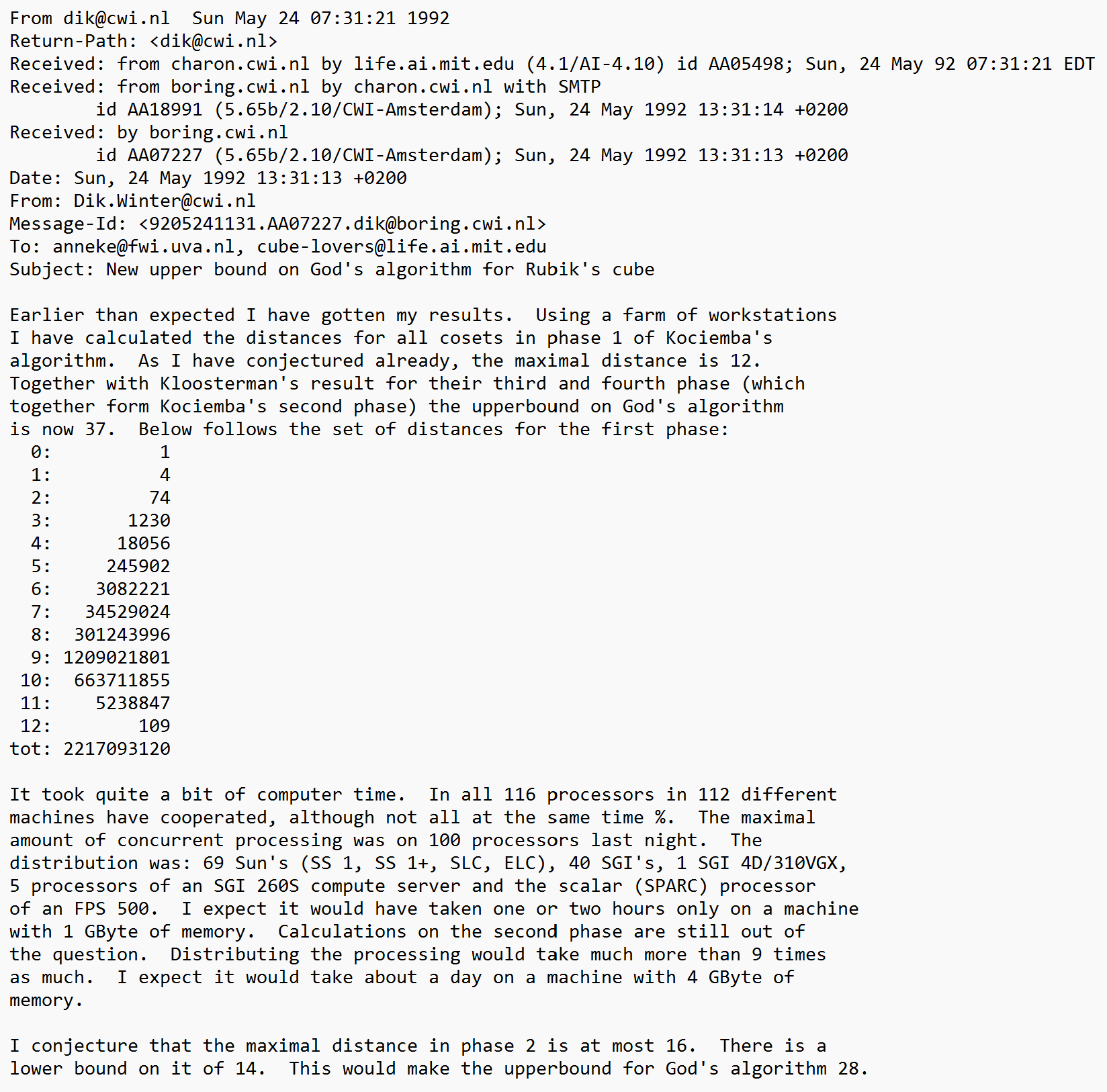
Dik Winter (1992)
On May 24, 1992, Dik Winter ran an extensive calculation of the first phase of Kociemba's algorithm. This provided a maximum distance of 12 moves. Winter combined this with the results of the final two phases of Kloosterman's algorithm, which was 25. The final result was a maximum distance of 37 [11, 4], which was the record at the time.
Silviu Radu (2005-2006)
In December, 2005, using the same method as Mike Reid, Silviu Radu reduced the maximum to 28 moves [12, 4]. This was accomplished by implementing methods to avoid the cube positions that had previously been calculated to require 29 moves.

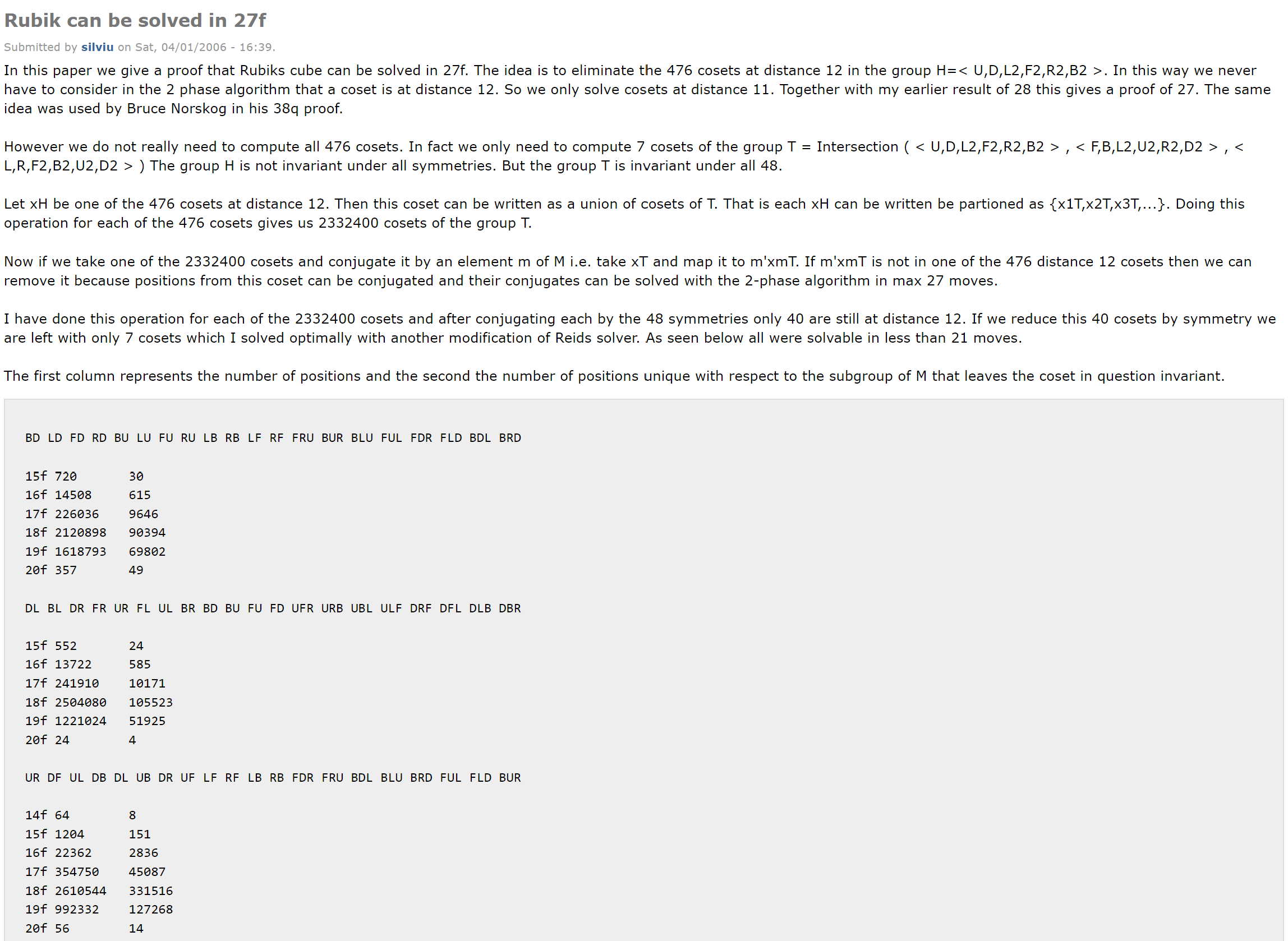
In 2005, Radu further decreased the number to 27 moves [13, 14, 4].
Daniel Kunkle and Gene Cooperman (2007)
The upper bound was further lowered to 26 in 2007, thanks to the work of Daniel Kunkle and Gene Cooperman [15, 16, 4].

Tomas Rokicki, Herbert Kociemba, Morley Davidson, John Dethridge (2007-2010)
In 2006, a team consisting of Tomas Rokicki, Herbert Kociemba, Morley Davidson, John Dethridge set out to further reduce the number [17].

Over a five month period in 2008, the team gradually reduced the maximum from 25 [18], to 23 [19], and then to 22 [20].



Finally, in July, 2010, the team proved that the maximum is 20 moves [21, 22, 4].

References
[1] D. Singmaster, in Notes on Rubik’s 'Magic Cube', Hillside, NJ, Enslow Publishers, 1981, p. 32.
[2] D. Singmaster, in Notes on Rubik’s 'Magic Cube', Hillside, NJ, Enslow Publishers, 1981, pp. 36, 39.
[3] M. Longridge, "Progress in Solving Algorithms," CubeMan, [Online]. Available: http://cubeman.org/dotcs.txt.
[4] T. Rokicki, H. Kociemba, M. Davidson and J. Dethridge, "God's Number is 20," cube20.org, 2010. [Online]. Available: https://www.cube20.org/.
[5] H. Kloosterman, "Rubik’s cube in 42 moves," in Cubism For Fun #25, 1990, pp. 19-22.
[6] M. Reid, "an upper bound on god's number," Cube Lovers, 29 April 1992. [Online]. Available: http://cubeman.org/cube-archives/cube-lovers/.
[7] H. Kociemba, "Close to God's algorithm," in Cubism For Fun, 1992, pp. 10-13.
[8] D. Winter, "Are we approaching God's algorithm?," Cubism For Fun, 4 May 1992. [Online]. Available: http://cubeman.org/cube-archives/cube-lovers/.
[9] M. Reid, "new upper bound," Cube Lovers, 22 May 1992. [Online]. Available: http://cubeman.org/cube-archives/cube-lovers/.
[10] M. Reid, "new upper bounds," Cube Lovers, 7 January 1995. [Online]. Available: http://cubeman.org/cube-archives/cube-lovers/.
[11] D. Winter, "New upper bound on God's algorithm for Rubik's cube," Cube Lovers, 24 May 1992. [Online]. Available: http://cubeman.org/cube-archives/cube-lovers/.
[12] S. Radu, "Solving Rubik's cube in 28 face turns," CubeMan, 22 December 2005. [Online]. Available: http://cubezzz.dyndns.org/drupal/?q=node/view/37.
[13] S. Radu, "New Upper Bounds on Rubik’s cube," Research Institute for Symbolic Computation (RISC-Linz), 2005. [Online].
[14] S. Radu, "Rubik can be solved in 27f," CubeMan, 1 April 2006. [Online]. Available: http://forum.cubeman.org/?q=node/view/53.
[15] D. Kunkle and G. Cooperman, "Twenty-six moves suffice for Rubik’s cube," Proceedings of the International Symposium on Symbolic and Algebraic Computation (ISSAC ’07), 2007. [Online]. Available: https://kociemba.org/math/papers/rubik26.pdf.
[16] D. Kunkle and G. Cooperman, "Harnessing parallel disks to solve Rubik’s cube," Journal of Symbolic Computation, 2007. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S0747717108001272.
[17] T. Rokicki, "In search of: 21fs and 20fs; a four month odyssey.," cubeman.org, 7 May 2006. [Online]. Available: http://cubezzz.dyndns.org/drupal/?q=node/view/56.
[18] T. Rokicki, "Twenty-five moves suffice for Rubik’s Cube," arXiv.org, 2008. [Online]. Available: arxiv.org/abs/0803.3435.
[19] T. Rokicki, "Twenty-Three Moves Suffice," cubeman.org, 29 April 2008. [Online]. Available: http://cubezzz.dyndns.org/drupal/?q=node/view/117.
[20] T. Rokicki, "Twenty-Two Moves Suffice for Rubik’s Cube," Mathematical Intelligencer, vol. 32, pp. 33-40, 2010, https://link.springer.com/article/10.1007/s00283-009-9105-3.
[21] T. Rokicki, H. Kociemba, M. Davidson and J. Dethridge, "The Diameter of the Rubik's Cube Group Is Twenty," Society for Industrial and Applied Mathematics, vol. 27, no. 2, pp. 1082-1105, 2014.
[22] T. Rokicki, "THE DIAMETER OF THE RUBIK’S CUBE GROUP IS TWENTY," rokicki.com, 2013. [Online]. Available: https://tomas.rokicki.com/rubik20.pdf.